Eigenvalue and Eigenvectors
First thing you should know is that a Matrix can be seen as a linear tranformation. Let’s see an example:
Let’s say that multiplication by $\mathit{A}$ transforms $\mathbf{x}$ into $\mathbf{b}$ and transforms $\mathbf{u}$ into the zero vector.
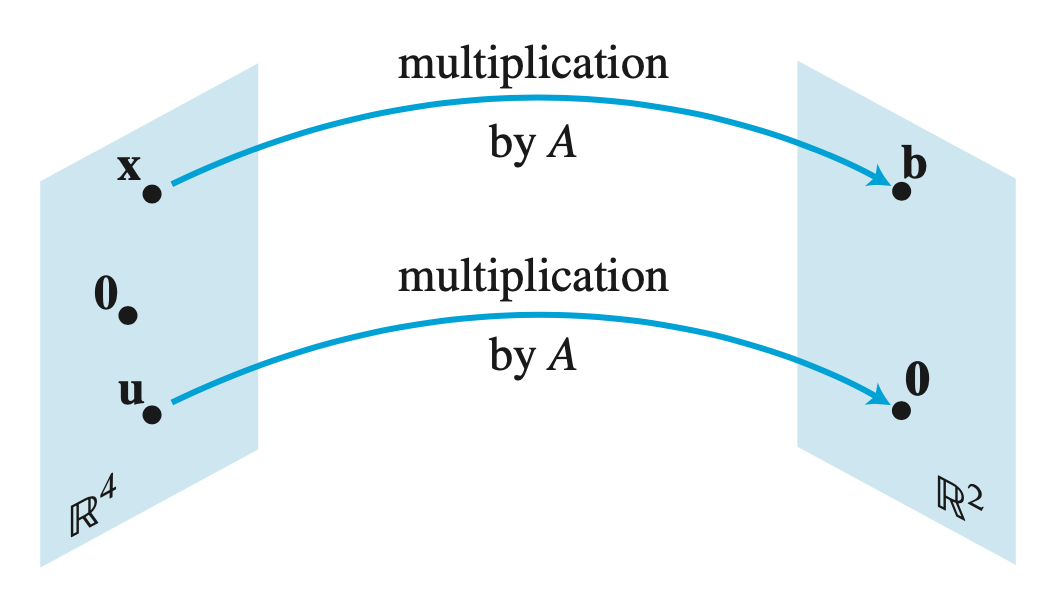
We can think of matrix $\mathit{A}$ as an object that “acts” on a vector $\mathbf{x}$ by multiplication to produce a new vector $\mathbf{b}$. Here, matrix $\mathit{A}$ is a correspondence rule that assigns each vector in $\mathbb{R}^3$ a vector $A(\mathbf{x})$ in $\mathbb{R}^2$. You can call it a mapping, or a function.
Every matrix transformation is a linear transformation, because:
$A(\mathbf{u} + \mathbf{v}) = A(\mathbf{u}) + A(\mathbf{v})$
$A(c\mathbf{u}) = cA(\mathbf{u})$
Let’s move to eigenvalues and eigenvectors. the word eigen origins from German, meaning “characteristic”. When we talk about eigenvalues and eigenvectors, matrix $\mathit{A}$ is usually square. In essence, a eigenvector $\mathbf{v}$ of a linear tranformation $\mathit{A}$ is a nonzero vector that, when $\mathit{A}$ is applied to it, it does not change the direction. Applying $\mathit{A}$ to the vector $\mathbf{v}$ only scales it, i.e. changes its length. We can write this condition like this:
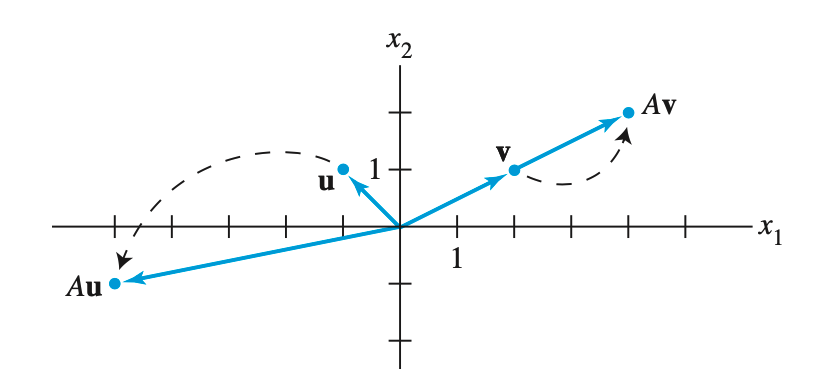A only scales vector v, without changing its directionA Personal Note
Well today I was doing some reading about RNN compression, and I came across something called “circulant matrix”. The word “circulant” pulled me back to the hot and humid classroom in Guangzhou. Then I found that I don’t remember a thing about it. So I think I should write down what I have learnt in the engineering classes, plainly explain what they mean, why they are useful etc, for the purpose of reminding myself because I’m too forgetful, and also for my brother who is also studying in the field of engineering. To anyone who reads this post, I hope it would be helpful.