Gumbel-Softmax

Why are we interested in Gumbel-Softmax?

Gumbel-Softmax makes categorical sampling differentiable. Why is that important? Because sometimes we want to optimize discrete or categorical choices with gradient methods. One of the applications is that we can use it in differentiable neural architecture search when we want to decide the operation on one edge.

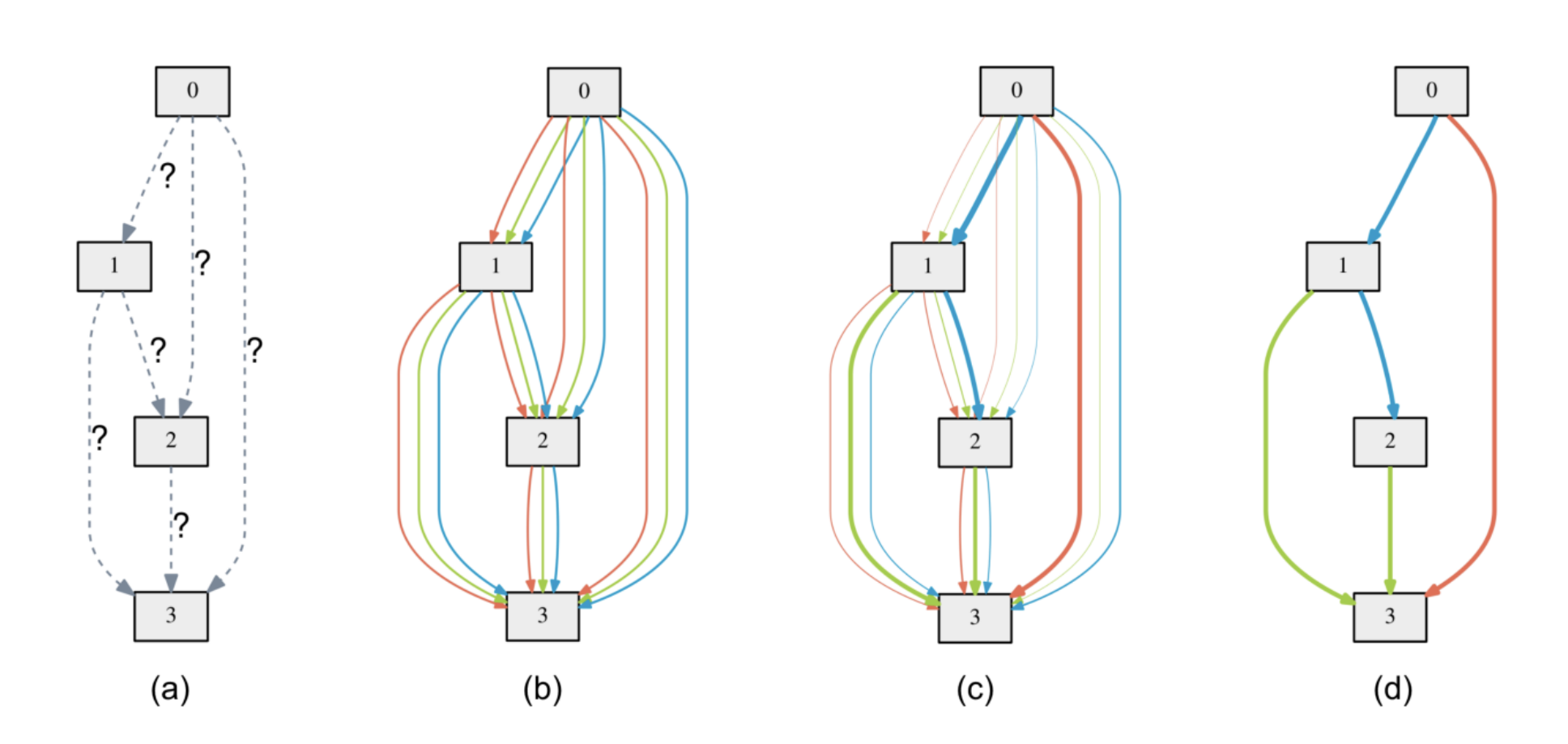DARTS: Differentiable Architecture Search

The original DARTS paper did not introduce Gumbel-Softmax. To decide which operation should be on one edge, it does the following things:

During search, the output of each operation is joined (weighted sum) with a group of learnable parameters (, , …, ), is the number of operation choices), like the color lines in the above figure.
When search is done, a final architecture is derived, meaning that we have to choose an operation for each edge. How do we do that? We use to choose the operation with the largest .

But, doing so causes a “gap”: the original network has a weighted sum of all operations during training, but the derived network loses all of the unchosen operation’s information, maybe the derived network has a different final performance than expected.

“If only we can train one network each time during search!” one might say. Indeed, selecting one operation for an edge during search instead of using a weighted sum is a good idea. But, sampling itself is not differentiable, we can’t update the parameters with gradient descent.

Don’t worry, Gumbel-Softmax is coming to rescue.

Gumbel distribution

First we need to understand what is Gumbel distribution.

Gumbel distribution stands for Generalized Extreme Value distribution Type-I. It is used to model the distirbution of the maximum of various distributions. Gumbel distribution is a particular case of the generalized extreme value distribution.

Gumbel distribution has two parameters:

: location
: scale, larger leads to fatter distribution.

The PDF of Gumbel distribution is:

$PDF(x) = \frac{1}{\beta} e^{-(a+e^{-z})}$

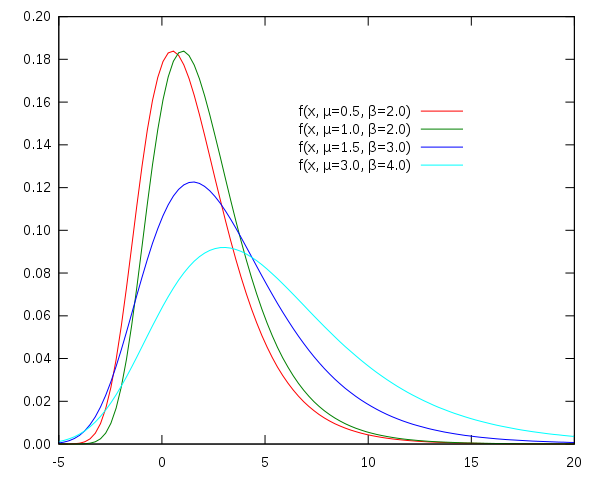
where . We see it has two exponential functions, so it is also known as the double-exponential distribution.

What is Gumbel-Softmax?

When we “choose an operation for one edge”, what we are doing is actually drawing a sample from a categorical distribution. A categorical distribution means a random variable can take the value of many discrete categories, with each case’s probability known.

Let’s say, we have a categorical variable with class probabilities , , , . To draw samples from the categorical distribution, we use the Gumbel-Max trick:

$z=\text { one_hot }\left(\underset{i}{\arg \max }\left[g_{i}+\log \pi_{i}\right]\right)$

where are i.i.d samples drawn from distribution. is defined as:

$\underset{x}{\arg \max } f(x)=\{x \mid f(x)=M\}=: f^{-1}(M)$

as is the maximum of . The problem here is is no way differentiable, so we use softmax instead, which is a softened argmax function, making it differentiable. So we get a softened , denoted as , the elements of are:

$y_{i}=\frac{\exp \left(\left(\log \left(\pi_{i}\right)+g_{i}\right) / \tau\right)}{\sum_{j=1}^{k} \exp \left(\left(\log \left(\pi_{j}\right)+g_{j}\right) / \tau\right)} \quad \text { for } i=1, \ldots, k$

This is the Gumbel-Softmax trick.

Here we added a temperature variable to control the softness of softmax.

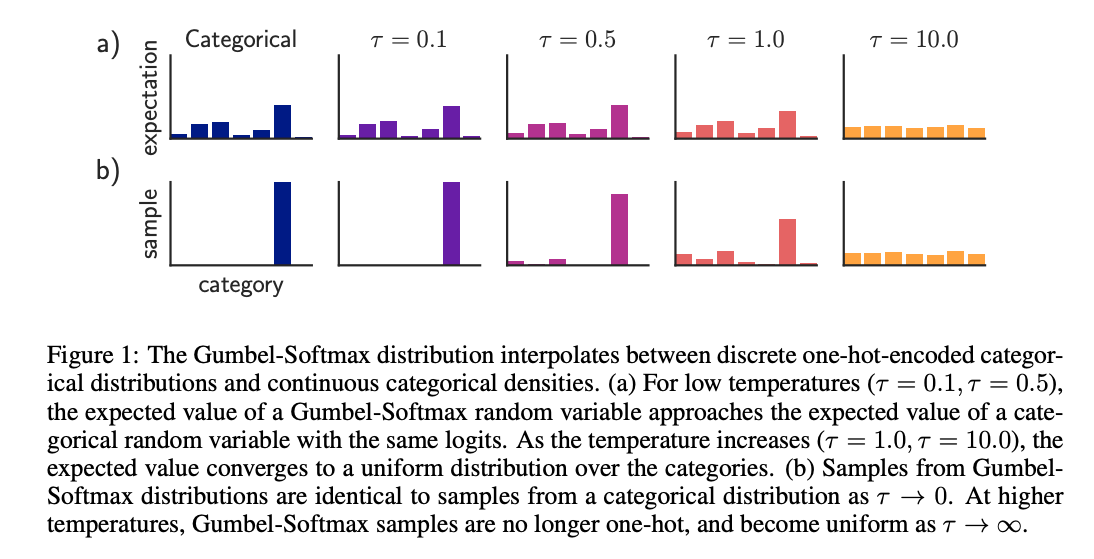
Let me explain. Softmax is just a normalized exponential function. At high temperature, every element is divided by a big number, making them all much smaller, so the absolute difference between every element is also smaller, so the distribution is closer to uniform. In contast, at low temperature (smaller than 1), dividing makes the elements bigger, so the difference between elements are also bigger, making the distribtion “sharper”.

We can think of as heating a crystal. Higher temperature melts the crystal, it becomes more soft (closer to uniform distribution). When it cools down, it becomes hardened and sharp.

We often use an annealing schedule with softmax, starting from a high temperature and gradually cooling it down. This is because we want every choice of operator sufficiently trained at early stage, and gradually forms a preference at later stage.

The Gumbel-Softmax gradient estimator

In some literature we may see the jargon “Gumble-Softmax gradient estimator”. It is well explained in the original paper:

“The Gumbel-Softmax distribution is smooth for , and therefore has a well-defined gradient with respect to the parameter . Thus, by replacing categorical samples with Gumbel-Softmax samples we can use backpropagation to compute gradients. We denote this procedure of replacing non-differentiable categorical smaples with differetiable approximation during training as the Gumbel-Softmax estimator.””

Straight-through Gumbel-Softmax gradient estimator

“Straight-through” means that only backward gradient propagation uses the differentiable variable, the forward pass still uses categorical variable.